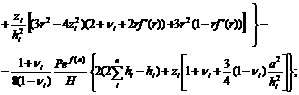ПОДРОБНАЯ ИНФОРМАЦИЯ
Заявку на получение дополнительной информации по этому проекту можно заполнить здесь.
|
Номер 19-045-03 |
|
Наименование проекта Изгиб круглых многослойных плит при осесимметричном нагружении силами, приложенными по экспоненциальному закону |
|
Назначение Ускорение расчетов при проектировании и в строительной механике |
|
Рекомендуемая область применения Строительство. Проектирование и расчет многослойных строительных конструкций. |
|
Описание Описание к ил № 19-045-03 Результат выполнения научно-исследовательской работы. Большое развитие получили исследования осесимметричного нагружения тел вращения или бесконечных пространства и полупространства. Изучение осесимметричного поля напряжений является одной из наиболее развитых областей теории упругости, уступающей по достигнутым результатам только плоской задаче. Особый интерес вызывают случаи локально приложенных нагрузок к плитам, опертым по контуру. Подобного рода ситуации весьма распространены в строительной практике и могут носить как статический, так и динамический характер. Например, складирование секций с кирпичом на перекрытии или удар поднимаемого груза о стену. Во всех указанных случаях действие нагрузки локализовано на незначительной части площади плиты, расположенной горизонтально или вертикально. Если для однородных плит при действии распределенной статической нагрузки решения имеются, то для слоистых плит при действии локальных нагрузок вопрос остается открытым. В данной работе рассматривается напряженно-деформированное состояние толстых многослойных плит при действии локальной нагрузки. В качестве локальной нагрузки примем нагрузку типа
Рис. 1. Рис. 2. При жесткой заделке цилиндрической поверхности должно выполняться равенство нулю радиальных перемещений
где
Рассмотрим изгиб круглой сплошной плиты состоящей изnслоев, приведенной на рис. 1, силамиp, приложенными по верхней поверхности первого слоя и изменяющимися по экспоненциальному закону
при
На границах слоев потребуем выполнения условия связности, а именно при
За функции
Соответствующая (6) функция
Положив в (7)
где
Таким образом, форма функций напряжений
Связь между радиальными перемещениями и, нормальными и касательными напряжениями и функциями напряжений
Подставляя функции (8) в формулы (9), составим выражения для напряжений и перемещений. Постоянные
Однако эти выражения не являются окончательными, их необходимо дополнить значениями, соответствующими силами
После составления выражений для напряжений и перемещений (10) присоединим их к ранее полученным:
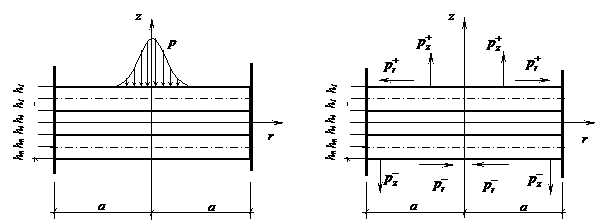
В формулах (10) и (11) под
В середине пролета
|
|
Преимущества перед известными аналогами Данный метод позволяет определять напряжения и перемещения в каждом слое многослойных плит при действии экспоненциальных нагрузок аналитическим методом |
|
Стадия освоения Метод проведен в лабораторных условиях |
|
Результаты испытаний Технология обеспечивает получение стабильных результатов |
|
Технико-экономический эффект Указанный метод расчета сокращает время расчета на 50 и более процентов и не требует применения сложной вычислительной техники |
|
Возможность передачи за рубеж Возможна передача за рубеж |
|
Дата поступления материала 10.06.2003 |
Инновации и люди

У павильонов Уральской выставки «ИННОВАЦИИ 2010» (г. Екатеринбург, 2010 г.)

Мероприятия на выставке "Инновации и инвестиции - 2008" (Югра, 2008 г.)

Открытие выставки "Малый бизнес. Инновации. Инвестиции" (г. Магнитогорск, 2007 г.)

Демонстрация разработок на выставке "Малый бизнес. Инновации. Инвестиции" (г. Магнитогорск, 2007 г.)
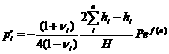 ;
;